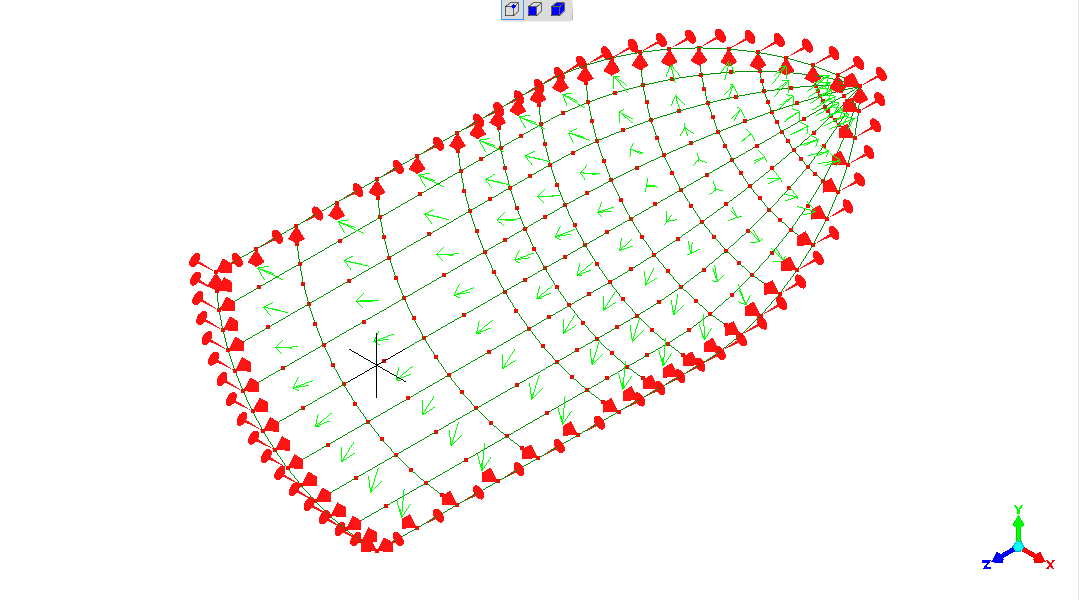
My model is making use of planes-of-symmetry again
The stress in the cylindrical body should be "sigma=Pr/t", whereas the stress in the hemispherical end-cap should be "sigma=Pr/2t". ie half the stress in the length of the shell. There must be some transition and some interesting stress-state; with some associated more complex elastic deformation pattern.
The cylinder and the sphere were chosen for having simple on-paper mathematical solutions to compare against. This case does not have a trivial on-paper solution. Never-the-less, the plausibility of the model can be checked against the cylinder and spare cases, of which it contains parts.
The model
isometric view of complete model

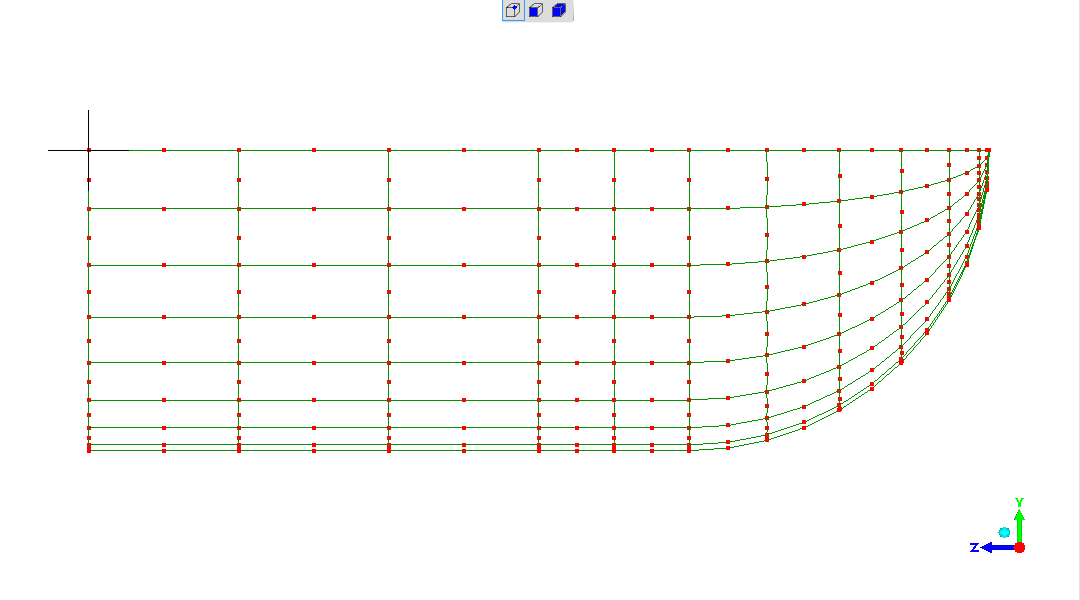
"x" side-view of mesh
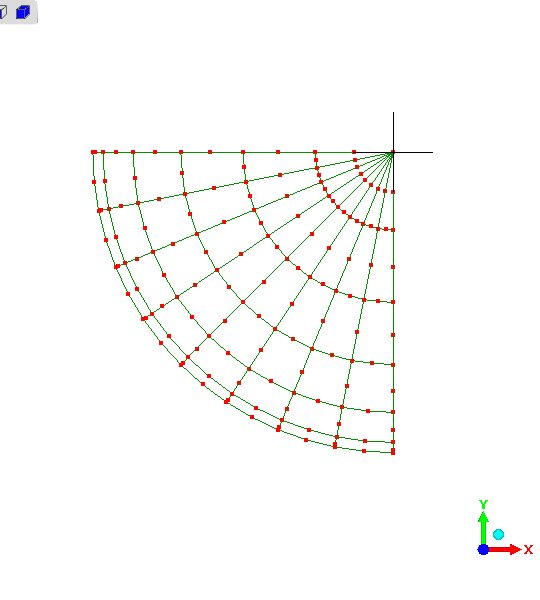
"z" end-view of mesh
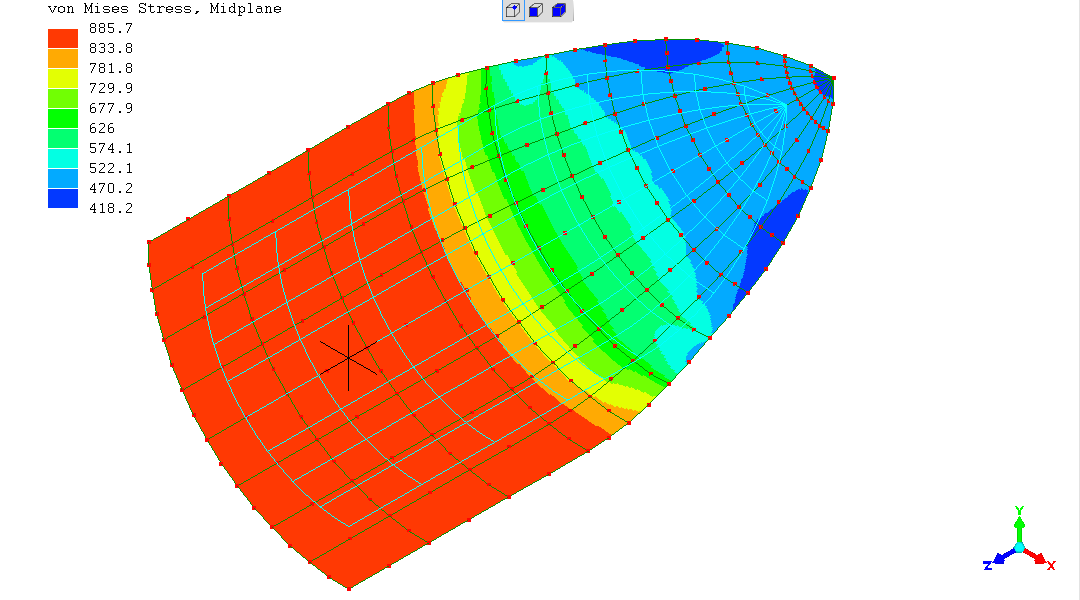
does indeed give a result which is interesting and a puzzling in several ways.
The result image shows exaggerated elastic deformation alongside the undeformed-mesh.
A "side" x-axis view shows the elastic expansion, and again all looks qualitatively reasonable (an error in the model would surely manifest is something absurd and obvious?!). The pattern of elastic deformation is interesting and begs future study.
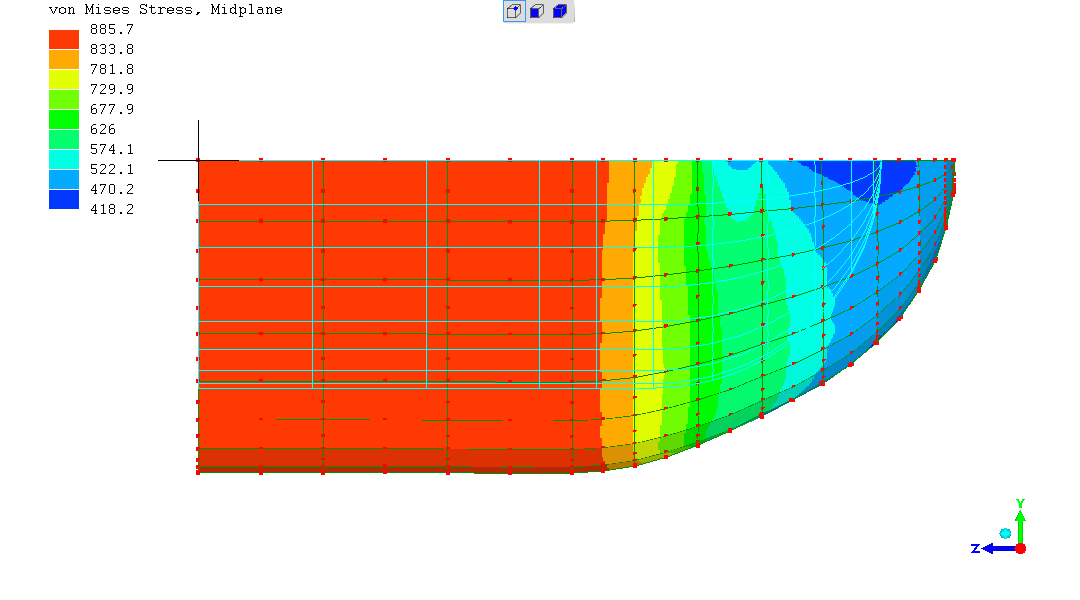
Reminder of the real shape (no exaggerated elastic deformation), with these stresses
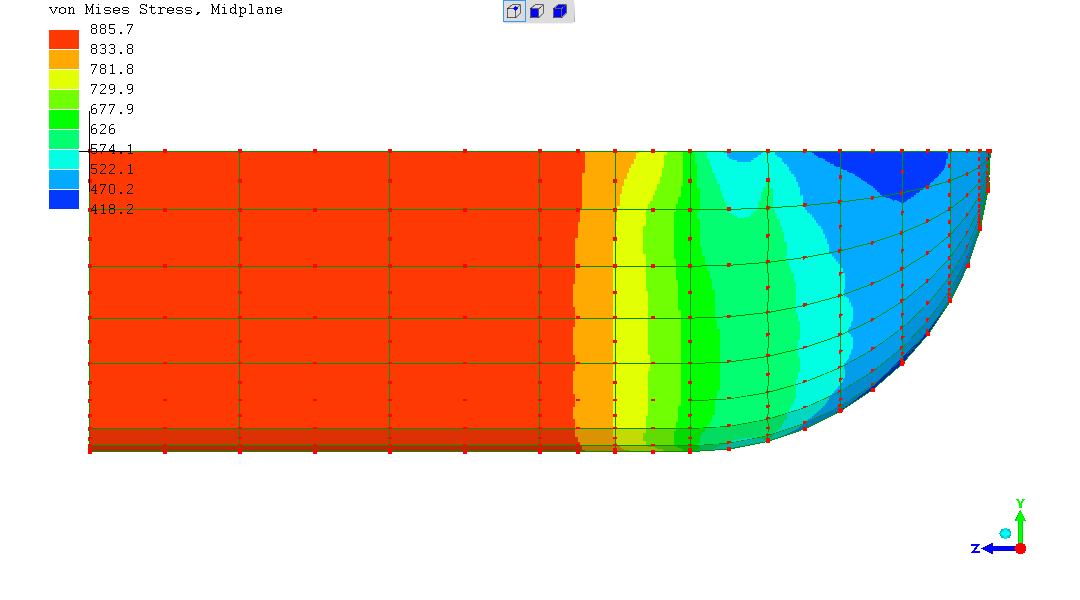
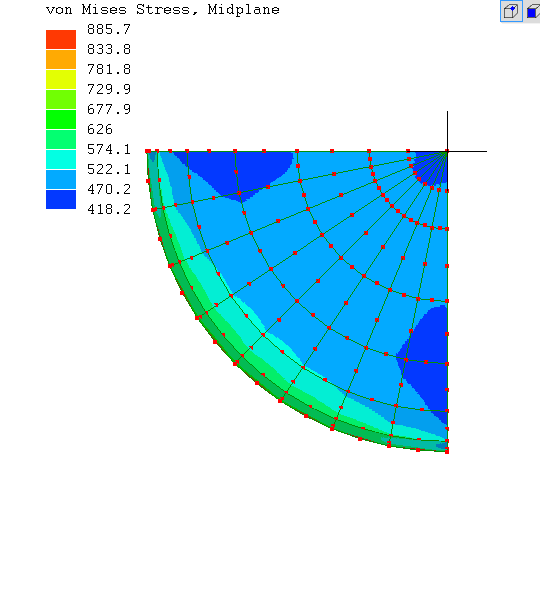
Vital next question...
What's going on with the stress in the cylindrical body of the vessel?
My instinctive first step was to increase the discretisation / refine the mesh - with this result
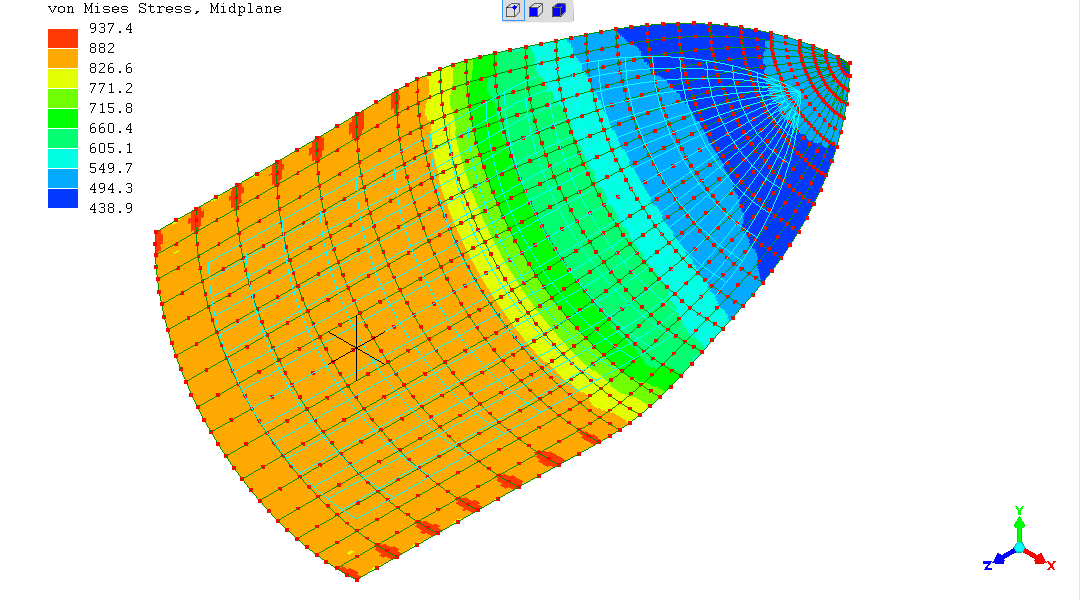
The stress in the cylindrical part is remaining at around "885" - unchanged from the previous simulation (the "red" areas appearing to be some "artifact" associated with the plane of symmetry - this is an "approximate" solution method!).
"Chopping-off" the hemispherical end of the vessel and re-running the simulation is revealing - the stress is back up very close to "1000".
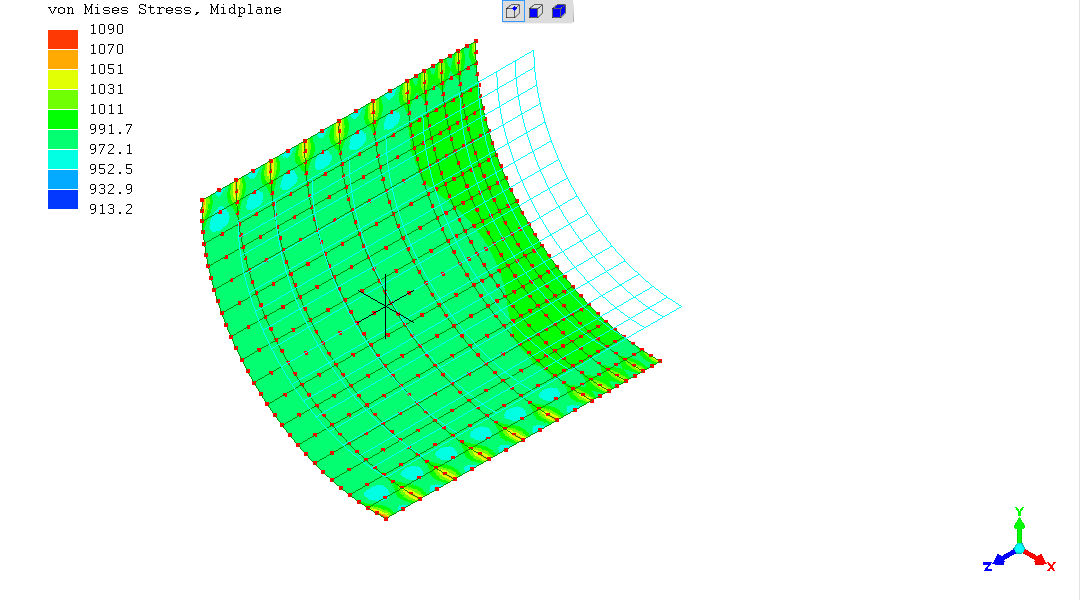
So it seems the model is properly implemented.
This result gives a hint...
The von Mises "deviatoric" stress
[von Mises - Wikipedia entry]
is most important, in general.
However, I've been getting lazy in my thinking with having modelled
the special phyically simplifying cases of a cylinder and a sphere.
This reveals all - it's a display of the Principal Stress. Right there on "1000" in the cylindrical region.
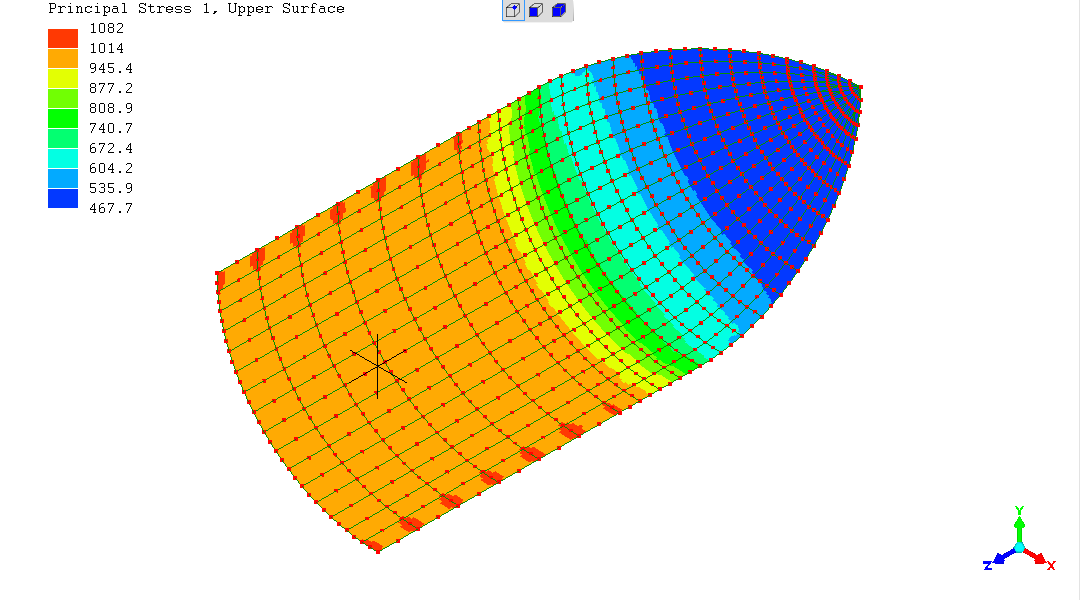
The von Mises deviatoric stress was simplifying to the mathematical
uniaxial value for "simple cylinder" and the spherical vessel (though
not for completely identical reasons!).
In this more complex case of simultaneous significant stresses in more
than one axis, although the shell is highly stressed, the deviatoric
component has gone down.
The stress(es) "sigma" (like an "o" with a trailing top tail)
with subscripts
For the cylindrical body of the vessel away from the end-cap effects,
(where P->pressure in vessel; r->radius of vessel; t=wall-thickness of vessel)
sigma_v = sqrt(0.5 * ((1000-500)^2 + (500-0)^2 + (0-1000)^2))
sigma_v = sqrt(0.5 * (500^2 + 500^2 + -1000^2))
sigma_v = sqrt(0.5 * 1.5Million)
so
von Mises stress, sigma_v = "866",
which fits with what is seen in the von Mises stress results for the
cylindrical body of the hemispherical-ended pressure-vessel.
[For the
spherical pressure-vessel
previously modelled, where
sigma_1="500", sigma_2="500" (both=Pr/2t) and sigma_3="0",
von Mises stress sigma_v = "500"; which is what is seen in those
simulations]
What are the real engineering consequences of these values and analyses?
It is familiar in engineering that, subject to simultaneous tensile
stresses along more than one axis, the tendency to yield, driven by
the deviatoric stress, goes down. "Yield" means to plastically
(permanently) deform ("bend", "change shape") - which can relieve
local high stresses.
Reduction in tendency to yield at high stresses accentuates a tendency
to brittle fracture
So, in summary, this simulation has indeed proved very interesting, thought-inducing and revealing.
(R. Smith, 20May2016)