To make these results easy to evaluate, I've use the same pressure for this sphere simulation as for the cylinder simulations. That pressure produces an expected stress, known from mathematics.
The equation for a sphere "sigma=Pr/2t" gives a shell stress of "500".
The hoop stress equation for cylinder "sigma=Pr/t" givs an expected
stress of "1000".
(for the same diameter and internal pressure, the stress in a sphere is
half that in a cylinder)
Struggling with the programs interface to highlight the plane-of-symmetry faces of a FEA model and define its "constraints", I made things easier for myself initially by defining a full sphere.

The "ring" of no-movement in Z-direction at z=0 is simply to anchor the model where intended, in this simulation and subsequent simulations, so as not be be "blown about" freely by computational error.
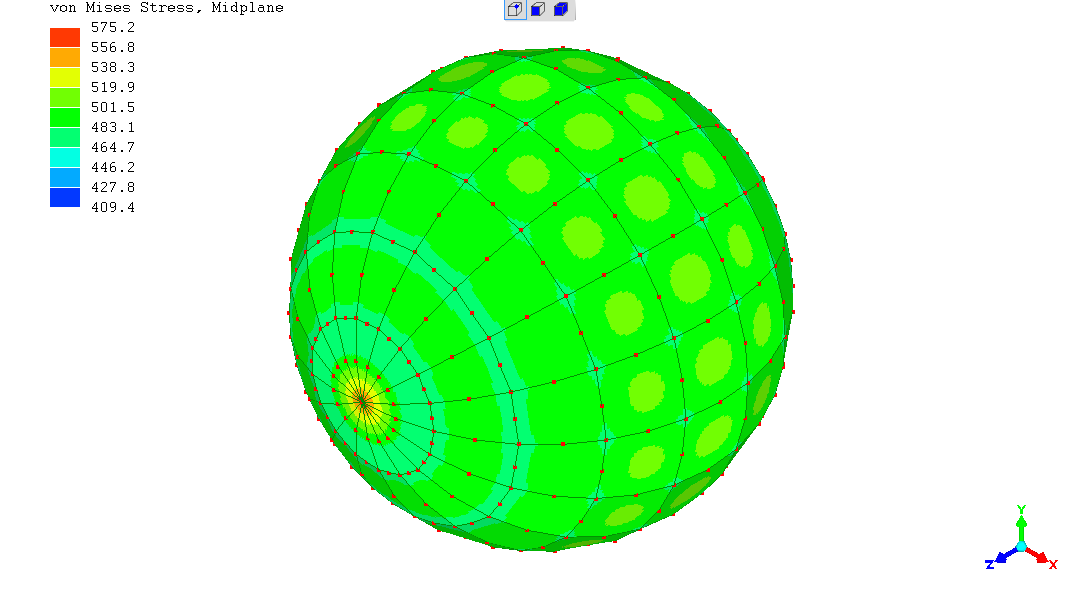
The stress in the spherical shell is the expected 500, but there are
"artefacts" at the Z-access locations of the sphere.
Simulating the full body, the simulation runs out of nodes for the
1300 "free version" limit if further mesh refinement is attempted.
Planes-of-symmetry were successfully implemented, for a quarter of the sphere representing the full model.
The "exaggerated elastic deformation" superimposed on the presentation
of the stress contours, alongside the undeformed-mesh, show the
expected radial elastic expansion. The overall stresses "500", also
as expected.
However, there are now "artefacts" along the edges of the represented
body, associated with the planes-of-symmetry.
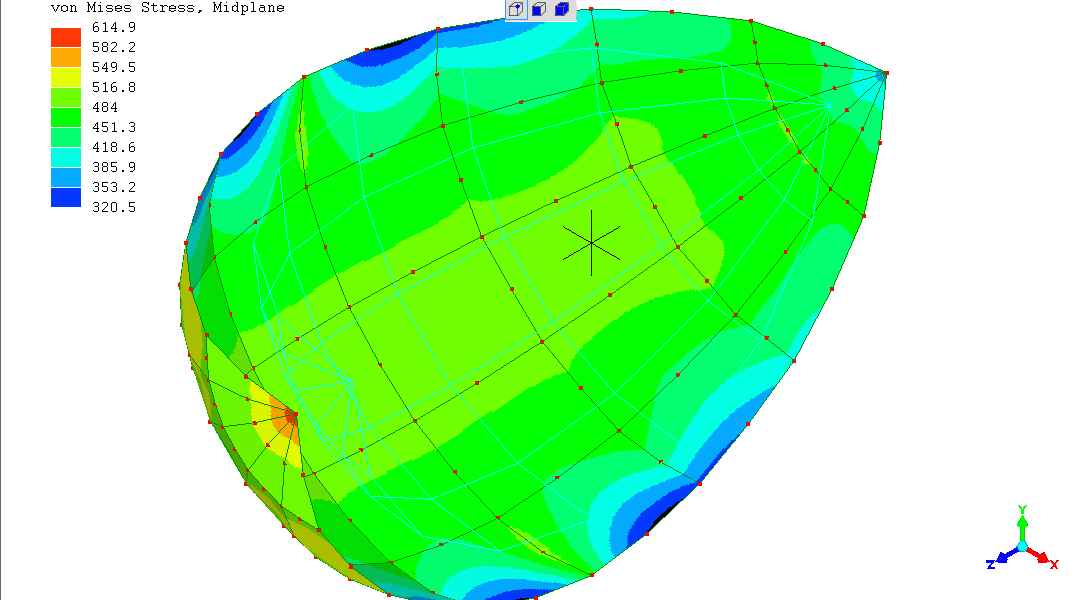
Refining the mesh by approximately halving the element size,
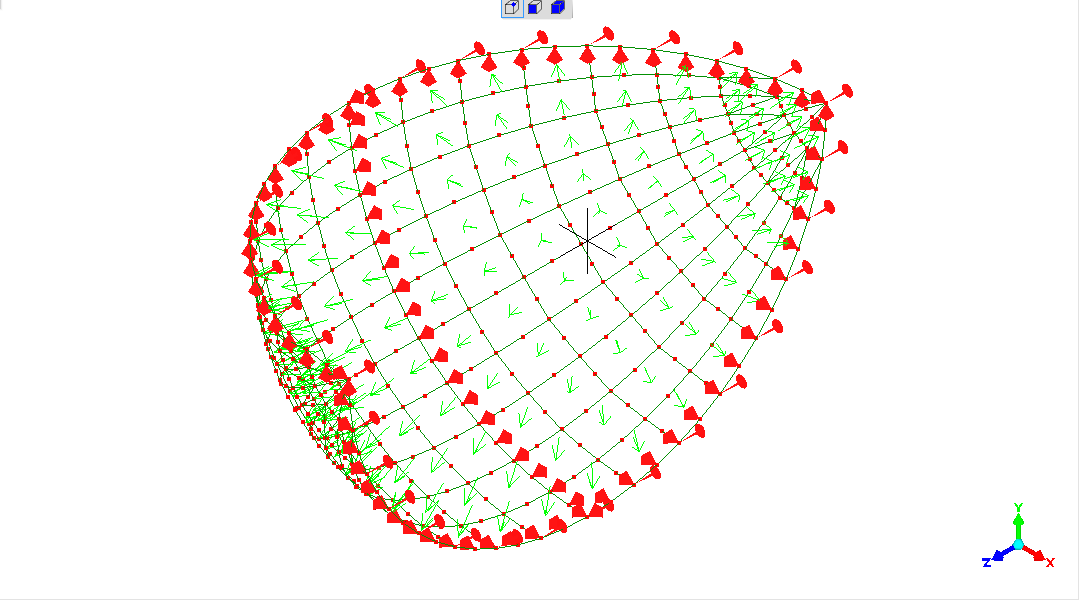
has produced a better result.
Note the colours of the stress scale are relative, so the "blue" of
this result is a closer result to "500" than in the previous, coarser,
simulation.
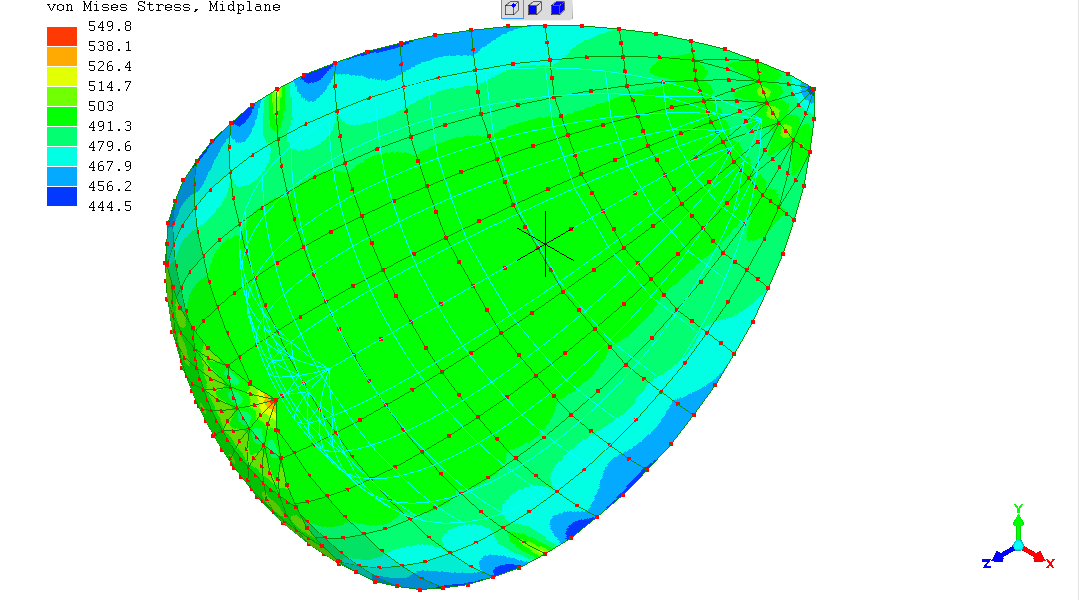
Running out of nodes, it's time to apply another plane-of-symmetry.
The third plane-of-symmetry has reduced the model representing the shere to only 1/8th of the sphere.
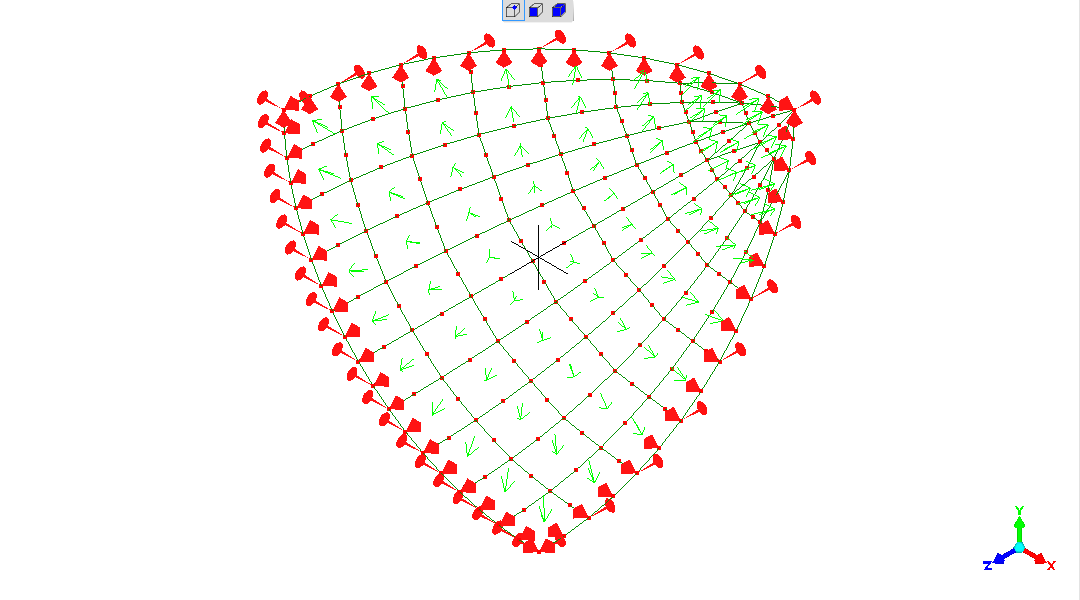
The similation appears good, though now the "artefacts" are around the new plane of symmetry, and no longer evident against the previous two planes of symmetry.
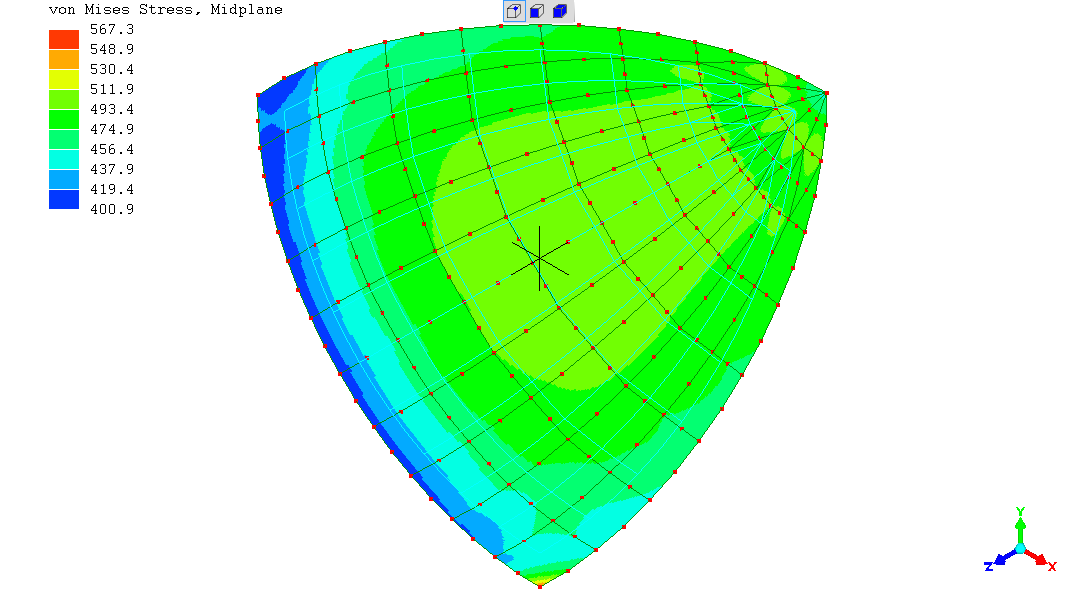
Further refining the mesh to 4 times the discretisation of the initial
"version 1" full sphere gives this following stress result.
The overall stress on the spherical shell is very exactly "500"; the
exact value from the mathematical equation known for this special case
of a spherical shell.
The artefacts on the plane-of-symmetry are further reduced in
magnitude.
Explanation why they exist in the first place???!
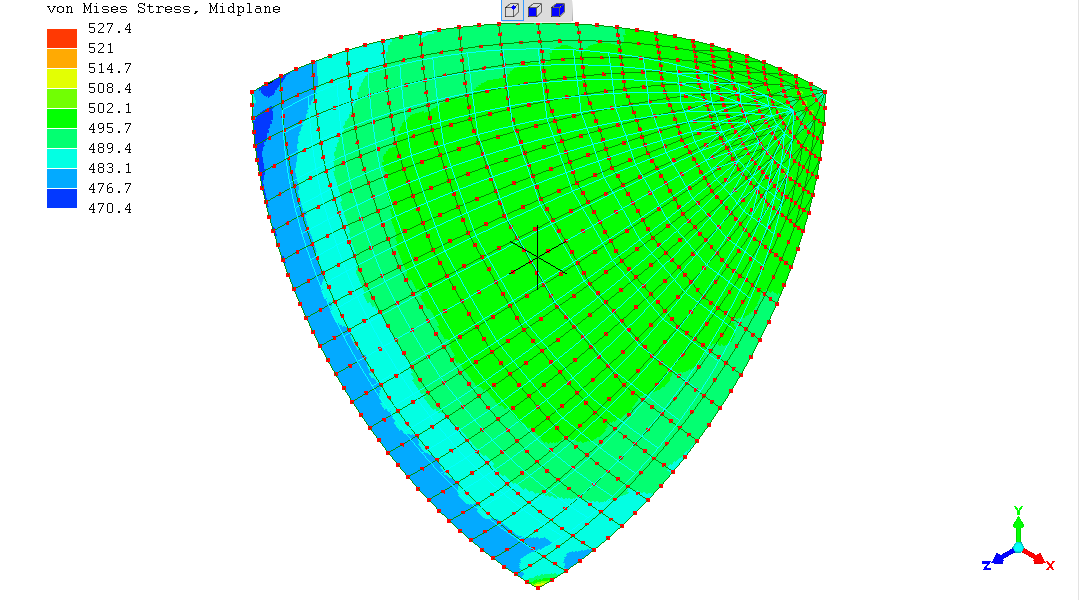
Inspecting a "z-axis" view, the artefact at the x=0 y=0 point on the sphere has almost completely disappeared at this discretisation.
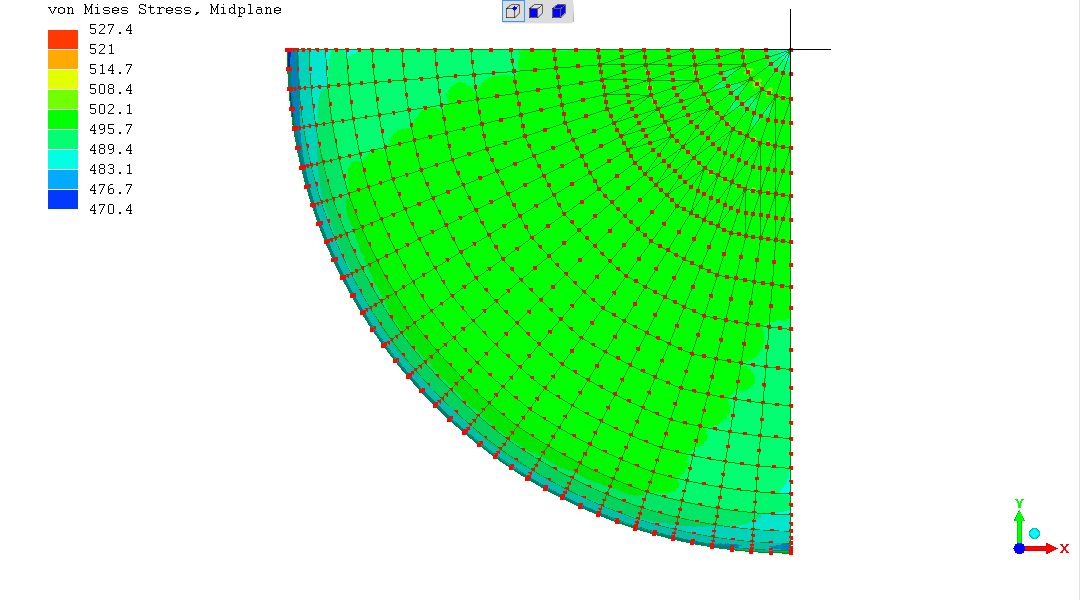
Overall, a promising result? However, reminding the reader of caveats about these being early-stage efforts whose results should not be relied upon.
(R. Smith, 20May2016)